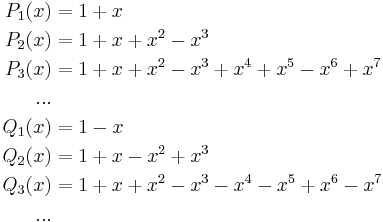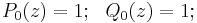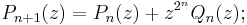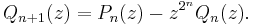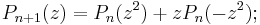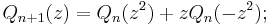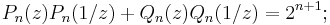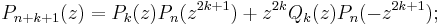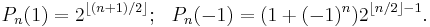Shapiro polynomials
In mathematics, the Shapiro polynomials are a sequence of polynomials which were first studied by Harold S. Shapiro in 1951 when considering the magnitude of specific trigonometric sums.[1] In signal processing, the Shapiro polynomials have good autocorrelation properties[2] and their values on the unit circle are small. The first few members of the sequence are:
where the second sequence, indicated by Q, is said to be complementary to the first sequence, indicated by P.
Contents |
Construction
The Shapiro polynomials Pn(z) may be constructed from the Golay-Rudin-Shapiro sequence an, which equals 1 if the number of pairs of consecutive ones in the binary expansion of n is even, and −1 otherwise. Thus a0 = 1, a1 = 1, a2 = 1, a3 = −1, etc.
The first Shapiro Pn(z) is the partial sum of order 2n − 1 (where n = 0, 1, 2, ...) of the power series
- f(z) := a0 + a1 z + a2 z2 + ...
The Golay-Rudin-Shapiro sequence {an} has a fractal-like structure – for example, an = a2n – which implies that the subsequence (a0, a2, a4, ...) replicates the original sequence {an}. This in turn leads to remarkable functional equations satisfied by f(z).
The second or complementary Shapiro polynomials Qn(z) may be defined in terms of this sequence, or by the relation Qn(z) = (1-)nz2n-1Pn(-1/z), or by the recursions
Properties
The sequence of complementary polynomials Qn corresponding to the Pn is uniquely characterized by the following properties:
- (i) Qn is of degree 2n − 1;
- (ii) the coefficients of Qn are all 1 or −1 , and its constant term equals 1; and
- (iii) the identity |Pn(z)|2 + |Qn(z)|2 = 2(n + 1) holds on the unit circle, where the complex variable z has absolute value one.
The most interesting property of the {Pn} is that the absolute value of Pn(z) is bounded on the unit circle by the square root of 2(n + 1), which is on the order of the L2 norm of Pn. Polynomials with coefficients from the set {−1, 1} whose maximum modulus on the unit circle is close to their mean modulus are useful for various applications in communication theory (e.g., antenna design and data compression). Property (iii) shows that (P, Q) form a Golay pair.
These polynomials have further properties[3]:
See also
Notes
- ^ John Brillhart and L. Carlitz (May, 1970). "Note on the Shapiro polynomials". Proceedings of the American Mathematical Society (Proceedings of the American Mathematical Society, Vol. 25, No. 1) 25 (1): 114–118. doi:10.2307/2036537. JSTOR 2036537
- ^ Somaini, U. (June 26 1975). "Binary sequences with good correlation properties". Electronics Letters 11 (13): 278–279. doi:10.1049/el:19750211. http://ieeexplore.ieee.org/Xplore/login.jsp?url=/iel5/2220/4236720/04236729.pdf?arnumber=4236729
- ^ J. Brillhart; J.S. Lomont, P. Morton (1976). "Cyclotomic properties of the Rudin–Shapiro polynomials". J. Reine Angew. Math. 288: 37–65.
References
- Borwein, Peter B (2002). Computational Excursions in Analysis and Number Theory. Springer. ISBN 0387954449. http://books.google.com/?id=A_ITwN13J6YC. Retrieved 2007-03-30. Chapter 4.